High Ceilings And Floors Part One

Identifying High Floors and Ceilings

Now that we have covered all of the basics regarding creating a model and projecting out scores, I think that it would be beneficial to discuss some strategies regarding player pool. I'm sure everyone here has ogne through the exercise of identifying key players to include or exclude from lineup optimization, but we can dig just a little bit deeper and start identifying which players are better for different contest types.

Contest Types

In general there are two main types of DFS contests, GPPs and Cash games.

GPPs

GPPs are going to be the big tournament that are very top heavy as far as prize distribution goes. Naturally, you will want much higher ceiling lineups for a GPP game, since there are masssive incentives to be the BEST and not just a good lineup. For these contests you will be taking bigger chances and swinging for the fences with high risk high reward plays.

Cash Games

Cash games are going to be double ups and 50-50s where it doesn't matter if you place 1st or 45/100 your winnings are the same. In this scenario, you are more incentivised to play it safe and craft a high floor, low risk lineup.

With these differences in mind, it stand to reason that you will want to take a different approach to creating lineups depending on what type of contest you are entering. Now, you may be thinking, who cares what contest i'm entering, if I have the best projections then I have the BEST lineup, end of story. While that hypothetical is true, no projection model is perfect, and no player performance is guaranteed. As is the case with projection models where you will want to incorporate many different statistical aspects of a players game, you will want to incorporate things beyond your straight projections when it comes to lineup construction. This is where things like ownership/chalk come into play, but for today we will be focusing on just the floor/ceiling aspects of the lineup construction puzzle.

How to Identify Floors and Ceilings?

We are going to look at a combination of 2 stats to help identify these attributes for players. These 2 statistics are going to be the mean and standard deviation of their scoring habits. For those of you who have not had to do much math in recent memory, the standard deviation is a measurement to quantify the variance or consistency of a dataset. In this case, it will be the consistency of a player's fantasy scoring. To explain standard deviation, we will be looking at a standard bell curve. A bell curve is what the normal distribution curve is typically referred to as, and is very useful to make this topic very easy to understand. Why don't we go ahead and create an arbitrary dataset so we can see how this concept plays out

#First thing we will need to do is import our packages we will be using, if you don't have any of these available
# you will need to pip install them

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

x = np.arange(-4, 4, 0.1)
y = norm.pdf(x,0,1)

Now what we just did by defining the x and y is create a range of x values ranging from -4 to 4, in increments of 0.1, and create corresponding y values that will follow a normal distribution curve with a mean of 0 and a standard deviation of 1. This is simply to make visual representation easy to comprehend, there is no significant meaning to those values other than to make all of our lives easier =]

Next up, we will define a figure using matplotlib, assign dimensions to the figure of 9x6, and then plot our x and y values within the figure. The figure dimensions are fairly arbitrary, but it will need to be big enough to read, without being unwieldy so feel free to alter this if you need to.

fig, ax = plt.subplots(figsize=(9,6))
ax.plot(x,y)

[<matplotlib.lines.Line2D at 0x1d973fe40c8>]

Now, we will go ahead and plot a vertical line at the mean of our dataset, which we already know to be 0 because we defined it as such. In addition, we will define an area under the curve to be shaded in. This specific area will become more relevant soon, but for now we just need to pick between -1 and 0 to shade in. We will define a range of x values to fill in and corresponding y values in much the same way we initially defined the values above.

fig, ax = plt.subplots(figsize=(9,6))
plt.axvline(x=0)
x_fill = np.arange(-1, 0, 0.001)
y_fill = norm.pdf(x_fill,0,1)

ax.plot(x,y)
ax.fill_between(x_fill,y_fill,0, alpha=.2, color='blue')

<matplotlib.collections.PolyCollection at 0x1d9757a3f48>

Personally, I don't like the default parameters of the graph not having 0 be the lower bound on the Y-axis so we're just going to make a quick adjustment, completely unnecessary but I think it looks a lot better this way. We will simply define y limits for the top and bottom of the axis here.

fig, ax = plt.subplots(figsize=(9,6))
plt.axvline(x=0)
x_fill = np.arange(-1, 0, 0.001)
y_fill = norm.pdf(x_fill,0,1)
plt.ylim(top=.45, bottom=0)
ax.plot(x,y)
ax.fill_between(x_fill,y_fill,0, alpha=.2, color='blue')

<matplotlib.collections.PolyCollection at 0x1d972a6a048>

Next up, as we continue to build out our bell curve, we will go ahead and plot vertical lines on all of our standard deviations away from the mean, which in this case we know will just be +/-1, +/-2, +/-3, and +/-4. Now is a good time to start thinking about how our bell curve is looking. We have our curve broken into sections by standard deviations, and the important aspect is going to be the number of standard deviations away from our mean. For instance, any point between 1 and -1 we are within 1 standard deviation of the mean. This type of thinking will become important.

fig, ax = plt.subplots(figsize=(9,6))
for num in  range(-4,5,1):
    plt.axvline(x=num)

x_fill = np.arange(-1, 0, 0.001)
y_fill = norm.pdf(x_fill,0,1)
plt.ylim(top=.45, bottom=0)
ax.plot(x,y)
ax.fill_between(x_fill,y_fill,0, alpha=.2, color='blue')

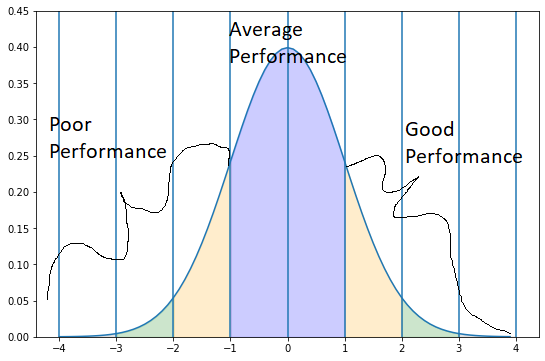
<matplotlib.collections.PolyCollection at 0x1d972d910c8>

I won't make you take all the steps to fill in each standard deviation steps, but in this next step i will be defining areas to fill in each standard deviation step and filling it in, then mirroring the same process on the opposite side of the mean. To interperate the following graph, the area shaded in blue is everything within 1 standard deviation of the mean, everything shaded orange is going to be between 1 and 2 standard deviations of the mean, everything in green is between 2 and 3 standard deviations of the mean, and everything in gray (too hard to see because it's such a small sliver) is greater than 3 standard deviations of the mean.

x = np.arange(-4, 4, 0.1)
y = norm.pdf(x,0,1)
fig, ax = plt.subplots(figsize=(9,6))
for num in  range(-4,5,1):
    plt.axvline(x=num)

plt.ylim(top=.45, bottom=0)
plt.ylim(top=.45, bottom=0)
ax.plot(x,y)
x1_fill = np.arange(-4,-3,0.001)
y1_fill = norm.pdf(x1_fill,0,1)
x2_fill = np.arange(-3, -2, 0.001)
y2_fill = norm.pdf(x2_fill,0,1)
x3_fill = np.arange(-2,-1,0.001)
y3_fill = norm.pdf(x3_fill,0,1)
x4_fill = np.arange(-1, 1, 0.001)
y4_fill = norm.pdf(x4_fill,0,1)
ax.fill_between(x1_fill,y1_fill,0,alpha=0.2,color='grey')
ax.fill_between(x2_fill,y2_fill,0, alpha=.2, color='green')
ax.fill_between(x3_fill,y3_fill,0,alpha=0.2,color='orange')
ax.fill_between(x4_fill,y4_fill,0, alpha=.2, color='blue')
x1_fill = np.arange(3,4,0.001)
y1_fill = norm.pdf(x1_fill,0,1)
x2_fill = np.arange(2, 3, 0.001)
y2_fill = norm.pdf(x2_fill,0,1)
x3_fill = np.arange(1,2,0.001)
y3_fill = norm.pdf(x3_fill,0,1)
ax.fill_between(x1_fill,y1_fill,0,alpha=0.2,color='grey')
ax.fill_between(x2_fill,y2_fill,0, alpha=.2, color='green')
ax.fill_between(x3_fill,y3_fill,0,alpha=0.2,color='orange')

<matplotlib.collections.PolyCollection at 0x1d9757a3f88>

Now that we have the bell curve nice and color coded, we can go ahead and start breaking down how this whole thing works. Basically the odds of an event happening are going to be dictated by how many standard deviations the event is away from the mean. This is driven by the 'normal distribution' of the data. There's some math mumbo jumbo that goes into it, and calculating the area under a curve, etc. However, when using normalized data it is pretty easy to conceptually understand. 34% of the area under the entire curve is between 0 and 1, aka within 1 standard deviation in the positive direction, and symmetrically 34% of the area under the curve is between -1 and 0, or within 1 standard deviation in the negative direction of the mean. Combine those together, and 68% of the area under the curve is within 1 standard deviation in either directin of the mean.

Another benefit of this type of distribution is it can be converted to probabilities as well. So we can also look at this as 68% of the time, the value will fall within 1 standard deviation of the mean. This can be extrapolated across the entire thing, so if you are looking at the odds a player will score between 1 and 2 standard deviations above the mean, that's going to be 34% + 14% = 48%.

In Review

Now if you're thinking ahead, you can start to think about how we can apply this to DFS. As I mentioned before, the standard deviation is a measure of the variance of the dataset. So now that we have seen how that plays out visually, a player with high standard deviation of scores, means that you will have a much larger range of scores that fall within the 68% between +/-1 standard deviations of the mean. Next time we will go over how to calculate this for players and how to analyze these data points into identifying players with a high floor and high ceiling.